发布时间: 2017年05月05日
知识点:资金时间价值
一、现金流量
1.现金流量的概念
◇现金流入量CI(流入经济系统或方案的资金);
◇现金流出量CO(流出经济系统或方案的资金);
◇净现金流量(NCF或CI-CO)t(同一时点上,现金流入量与现金流出量之差)。
2.现金流量图
◆现金流量的三要素:大小;方向(流入或流出);作用点(发生时间-某一计算期的期末)。
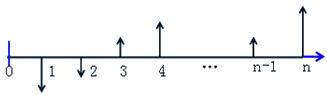
图3-1现金流量图
◇现金流图的绘制规则:横轴;箭线方向;箭线的长度;箭线与横轴的交点(现金流量发生的时点)。
3.现金流量表
二、资金时间价值的计算
(一)资金时间价值的概念
◆含义:资金因参与流通,随着时间的延伸而产生增值(利润或利息)的现象或属性。
◇实质(增值-利息):资金提供者,补偿(回报);资金使用者,代价。
(二)资金时间价值计算的种类
◇三个:等值(等效值);未来值(终值);现在值(现值)。
(三)利息和利率
◇有关概念:本金;利息;利率。
1.单利法
◇利不生利:I=P×n×i(式3-2)
◇例3-1
2.复利法
◆利上加利:
表3-2复利法计算原理
| 期初本金 | 期内利息 | 期末终值(复本利和) | |
| 第1期 | P | P×i | P+P×i=P(1+i) |
| 第2期 | P(1+i) | P(1+i)i | P(1+i)+P(1+i)i=P(1+i)2 |
| … | … | … | … |
| 第n期 | P(1+i)n-1 | P(1+i)n-1i | P(1+i)n |
◇例3-2.
◆在上述两种计息方法中,如果未做特殊说明,应当选择(默认)复利法(计息)。
(四)实际利率和名义利率
【补例1】某人向您借款10万元,借期2年,每个季度计息一次,季度利率是2%.则到期后的利息应为多少?
【解】该例题,有以下不同的算法,并引发实际利率和名义利率的区别:
第一种算法:100000×(1+2%×4×2)=116000元,利息为16000元;
第二种算法:100000×(1+2%×4)2=116640元,利息为16640元;
第三种算法:100000×(1+2%)4×2=117165.94元,利息为17165.94元。
◇题中利息的差异,主要源于1年内的各个计息周期(季度)之间是否复利计息。其中,第一种算法中的年利率8%,属于名义利率;第三种算法中的利率=,属于年实际利率。
1.名义利率
◇含义:计息周期利率乘以每年计息的周期数。例如,上例中的2%×4=8%,其各个季度之间属于单利计息。
2.实际利率(有效利率)
◆如果年名义利率为r、一年内的计息周期次数为m,则年实际利率(i)可按下式计算:
![]() (式3-8)
(式3-8)
对于补例而言,年实际利率为8.24%.
【例3-3】某公司存入银行10万元,年利率为2.79%,共存5年,按复利每半年计息1次,问存款到期后利息?
【解】已知P=10,r=2.79%,m=2,n=5
①按年实际利率计算:由i=(1+2.79%/2)2-1=2.81%,则F=10×(1+2.81%)5=11.486(万元)。
②按计息周期利率计算:2.79%/2→n=10(个半年);
F=10×(1+2.79%/2)10=11.486(万元)。
◆于是,利息=11.486-10=1.486(万元)。
3.实际利率的讨论
![]()
①当m=1时,实际利率(i)等于名义利率(r);
②当m>1(计息周期不足1年)时,实际利率(i)将大于名义利率(r),而且m越大,二者相差也越大;
③m<1,只有数学意义,没有经济意义。
◆一年内的各个计息周期之间采用单利计息,属于名义利率;各个计息周期之间是复利计息,则为实际利率。而且,未来应该选择实际利率(式3-8)。
(五)资金时间价值计算的基础概念和符号
1.现值(P):资金发生在(或折算为)某一时间序列起点时间的价值,或相对于将来值的任何较早时间的价值;
2.终值(F):资金发生在(或折算为)某一时间序列终点时间的价值,或相对于现在值的任何较晚时间的价值;
3.等额年金或等额资金(A):发生在或折算为某一时间序列各个计算期期末(不包括零期)的等额资金的价值。参见图3-2,或补充的图3-1。
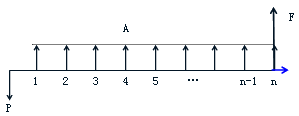
补图3-1:现值、终值与等额资金的关系图
(六)复利法资金时间价值计算的基本公式
1.一次支付的终值公式(已知P,i、n,求F)
◆一次支付的背景下,已知计息周期利率i,则n个计息周期(年)末的终值F,可按下式计算:F=P(1+i)n(式3-9)
◆其中,(1+i)n为一次支付的终值系数,记为(F/P,i,n)或理解为(F←P,i,n)。它可以描述用途或功能(做什么);若有关数据已知,可得出相应的数值(做到什么程度)。
2.一次支付的现值公式(已知F,i、n,求P)
◆由终值公式(3-9)的逆运算,可得现值P的计算式为:P=F(1+i)-n(式3-10)
◆其中,(1+i)-n为现值系数,记为(P/F,i,n)。
【例3-4】某公司计划2年以后购买100万元的机械设备,拟从银行存款中提取,银行存款年利率为2.25%,问现应存入银行的资金为多少?
【解】已知F=100万元,n=2年,i=2.25%
则P=F(1+i)-n=100×(1+2.25%)-2=95.648(万元)
◆将不同时间的资金进行折现或称贴现,更加常用。
3.等额资金的终值公式(已知A,i、n,求F)
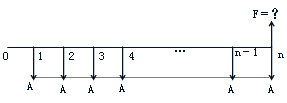
图3-4等额资金终值的现金流量图
◆其计算(推导)式为:
◆在式3-11中,![]() 称为年金终值系数,记为(F/A,i,n)。
称为年金终值系数,记为(F/A,i,n)。
【例3-5】如果从1月份开始,每月月末存入200元,月利率为1.43‰,求年底积累的储蓄额?
【解】由式3-11,则F=200×12.0948=2418.96(元)
◇形象记忆:若现在开始每年等额存入一笔钱(存款、养老保险),则到若干年可一次性地取出多少钱?
4.等额资金偿债基金公式(已知F,i、n,求A)
◆由等额资金终值公式(3-11)的逆运算,可得偿债基金公式为:
![]() (式3-12)
(式3-12)
◆其中,![]() 称为偿债资金系数,记为(A/F,i,n)。
称为偿债资金系数,记为(A/F,i,n)。
◇形象记忆:为了未来N年后一次性支取的定额养老金,现在开始应等额存入的款项;图3-5.
5.等额资金的回收公式(已知P,i、n,求A)
◆由“P→F”(式3-9)和“F→A”(式3-11),可有等额资金回收公式(参见图3-6):
![]() (式3-13)
(式3-13)
【例3-7】P=100万元,i=10%,n=5.则A=?
由式3-13及已知条件,则A=26.38万元
◇形象记忆:在住房按揭贷款中,已知现在的贷款总额、利率,求一定期限内的月供或年供。
6.等额资金的现值公式(已知A,i、n,求P)
◆由等额资金回收公式(式3-13)的逆运算,可得等额资金的现值公式:
![]() (式3-14)
(式3-14)
◆其中,![]() 称为年金现值系数,记为(P/A,i,n)。
称为年金现值系数,记为(P/A,i,n)。
【例3-8】A=100万元,i=5.76%,n=6年。P=?
由式3-14及已知条件,则P=495.46(万元)
◇形象记忆:先存后取的养老金模式(以后若干年内,每年领取年金若干,求当初存入多少钱)。
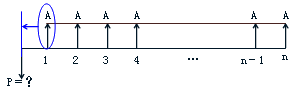
图3-7等额资金现金流量图
◆注意:P与首个A,只能间隔一个计息周期。
编辑推荐: